- 联系方式:1761430646@qq.com
- 菜狗摸索,有误勿喷,烦请联系
1. 回溯
1.1 一些点
-
要知道回溯其实就是暴力,但是与正常的多重套娃for或者while循环相比,它通过条件判断自主完成多重循环的套娃,即通过一套固定的模板我们不用事先决定好循环的层数,而正常的循环套娃需要
-
回溯是递归的产物,个人理解回溯跟递归的差异点在于正常来说递归是一定往深处走,知道走到基准情形不满足的情况才会停止再往回走,而回溯可以通过一些条件判断–即剪枝操作,在走到一定深度时其实就可以往回走,不必再往深处走,那样没意义了
-
任何回溯的执行过程都可以抽象成多叉树的dfs过程,脑海中一定要有这个概念
-
回溯就是在枚举所有可能,结合多叉树的结构,回溯有一套固定的模板
-
横向遍历其实就是在遍历多叉树的一层
-
纵向遍历就是往叶子结点方向走(通查来说叶子结点往往都是目标所求)
-
void backtracking(参数){ if(终止条件){ 存放结果; return; } for(选择: 本层集合中的元素){ 处理结点; backtracking(路径,选择列表); // 回溯 | 递归 回溯,撤销处理结果; } }
-
-
回溯可以解决大概5大类问题
1.2 例子
-
以一个组合问题为例,重点是抽象成树的结构 + 模板,其他问题都是在此基础上多加限制条件
-
问:给定一个长度为4的数组[1, 2, 3, 4]–数组内元素不重复,求长度为3的各种组合情况(不能含有重复,如[1, 2, 3] 跟 [2, 1, 3])
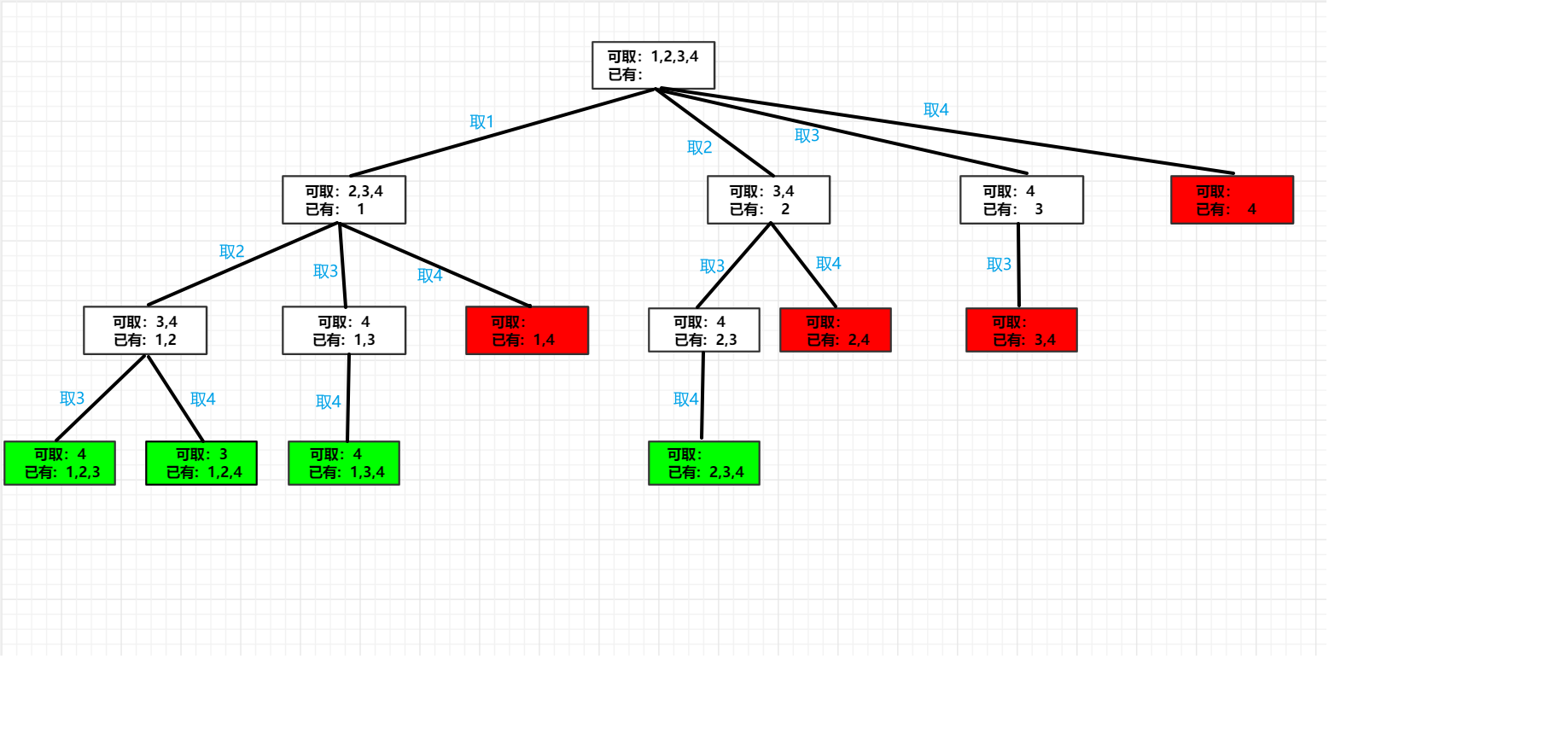
- 假设我们用来临时存放已有元素的集合名为tem
- 一开始的时候,我们可以取1或者2或者3或者4,也就是在横向遍历存放可取元素的集合
- 每当取完一个数后,进入下一层的递归
- 判断此时是否已经满足条件,没有满足则继续上述过程
- 最后到了叶子结点或者是满足了终止条件,则将临时集合tem中所有元素[1, 2, 3]加入结果集中
- 接着回去,返回到上一层,也就是回到父亲结点,一个很重要的点时每次返回上一层时都要把你之前做过的动作撤销掉(精髓所在)–在这里是指比如把元素3放入了临时集合[1, 2, 3]中,然后进入下一层的递归,那么你返回上一层时就要把3从临时集合中删除掉[1, 2](很容易实现这一点,相当于add()元素到集合末尾,然后remove()最后一个元素)
- 如果返回到上一层时没有撤销动作,那么后果很严重,比如得到目标结果[1, 2, 3]后回到上一层后,此时tem存放的还是[1, 2, 3],接着取4进行递归,又到了叶子结点,但此时tem存放的是[1,2, 3, 4],后面就是[1,2,3,4,3],[1,2,3,4,3,4],[1,2,3,4,3,4,4]…回溯就是这个多叉树的中序遍历,没有撤销动作只会每一次都蝴蝶效应的导致后面tem的长度只会越来越长,元素重复,所以会造成后面永远不会有别的答案产生。
-
提问一:为什么我第一次取了2之后,后面就不能在取1?
-
这是组合问题,题目要求了答案不能重复
-
在同一层中,1 在 2 的前面,根据回溯就是这个多叉树的中序遍历,我们知道在开始取2然后进行递归之前,一定会先把取1然后进行递归这个动作先完成,如图所示,那么取1后把包含排在它后面的数的所有可能它都会尝试过,如果取2后允许再取比2排在前面的数–1的话,那么就会产生重复的过程,做没有意义的事情,浪费时间和空间复杂度。
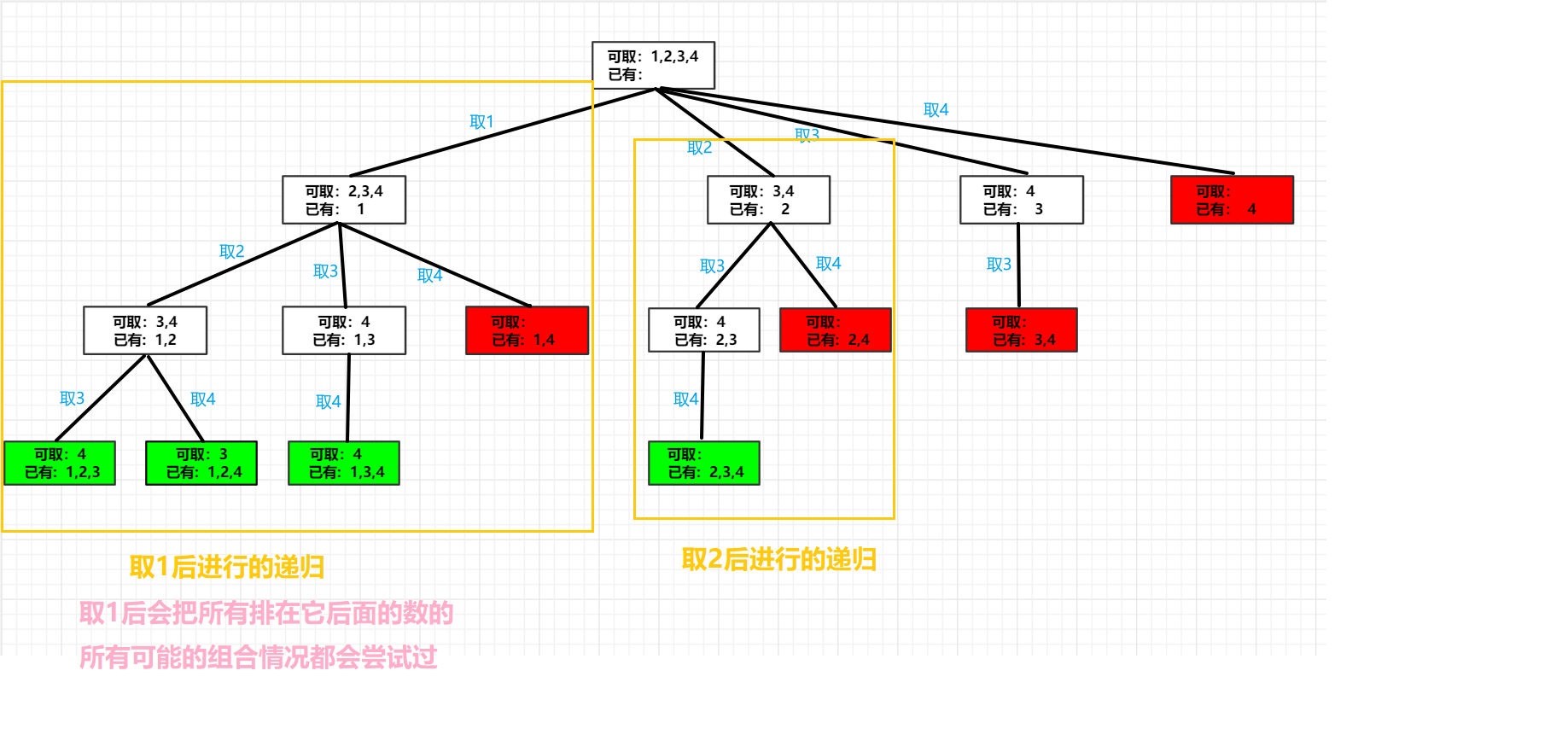
-
-
提问二:存放可取元素的集合怎么来记录?
-
其实我们可以用题目给出的原本存放所有元素的集合[1, 2, 3, 4]即可,只是每一次用一个变量start来标识同一层的启始遍历位置,由上述可知不用再理会比起始位置还要靠前面的那些元素
-
也即参数中应该含有
-
void backtracking(List<Integer> origin, int start)
-
-
需要用临时集合tem来存放元素,所以参数中应该含有
-
void backtracking(List<Integer> origin, int start, List<Integer> tem)
-
-
当然,临时集合tem只是一个指针指向而已,实例其实也就只有一个,所以不一定要写在参数那,我们可以把它定义一个全局变量
-
-
提问三:可以剪枝?
- 可以
- 比如我们已有元素2,可取元素为[3, 4],当我们选择4的时候发现选完后已有元素[2,4]长度不满足于 == 3,,后面再进行递归时其实已经没有元素可以选择了,也就是选4时根本没有并要进行下一层的递归,所以我们可以在选取元素的时候进行剪枝
- 具体剪枝操作为 当前已有元素长度 + 还可以再选择的元素长度 >= 目标长度
- 具体代码实现为
tem.size() + (origin.size() - i) >= target- i 为当前遍历到的集合下标
- target为目标长度
1.3 例子衍化-原集合有重复元素
-
比如我们的集合是[1, 2, 3, 3, 4, 5, 6, 6, 6,7],也即集合有了重复元素,但要求结果集合不能重复,并且结果集合内元素也不能重复
- [1, 3, 3] F
- [2, 1, 3] [1, 2, 3] 只能有一个是T
-
很重要的一点:这里一定先要对原集合排序,上面虽然我给出的是元素是递增的集合,但是实际过程中集合元素大概率是无序,但针对上面那里来说,还是不用排序,因为集合内每一个元素都不会重复保证了这一点,就我每次获取到元素不会重复
-
而这里题目要求结果集合内元素不能重复,再加上原集合内是存在重复元素的,所以为了方便我们处理,一定先排序
-
原集合排序后会有一个很重要的特征,就是元素重复会是连续发生的,我们可以通过此特征来排除重复元素的选择
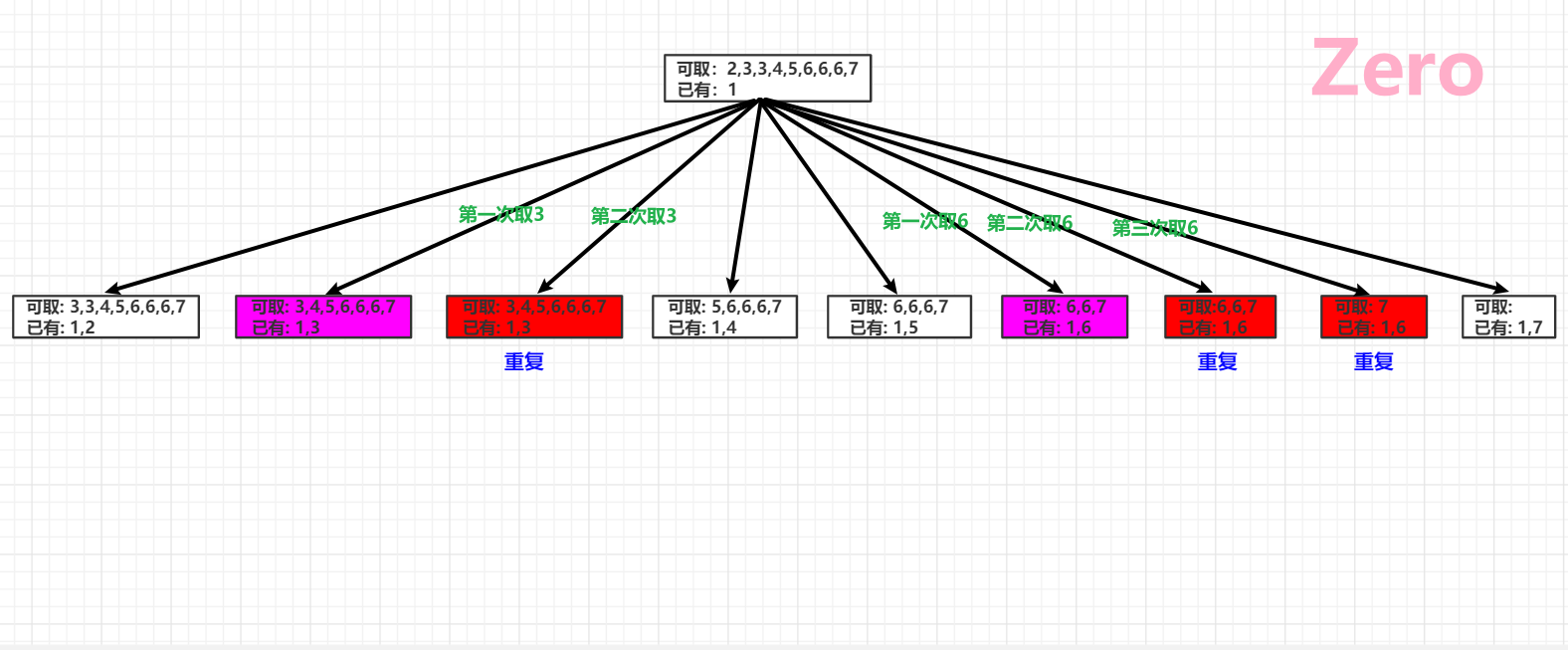
-


